What are Imaginary Numbers?

Edited by Kimberley Chee.

Introduction

Many of us would have heard this in our journey of learning mathematics: “this is a complex area that you will learn as you progress”. When I was first introduced to solving problems that involved quadratic equations, using the factoring approach or completing the squares seemed fairly straightforward. Moving on to the more complex equations called for the use of the quadratic formula. Most of the time, I got a normal answer with the regular positive roots, leading me to believe that the ‘perfect’ quadratic formula would always return a whole number or positive root answer. But one day when I attempted to solve a quadratic equation using the quadratic formula, I noticed that I got a negative root in my answer. I had a calculator at the time and I decided to plug the equation into my calculator to find x and I got the exact same answer as when I worked it out on paper.

At first, I decided to ignore the outcome and move on to other questions. But my curiosity got the better of me, and I asked my teacher about how to make sense of the answer. I was told that this involves the use of imaginary numbers, something we will be taught much later…

Based on my own exploration, this article introduces the concept of imaginary numbers, some arithmetics involving these numbers, and eventually how they contribute to things we use or do in our daily lives.

Types of Numbers

Let us start with a quick view of the types of numbers we deal with. The diagram below summarises these together with some examples of each:

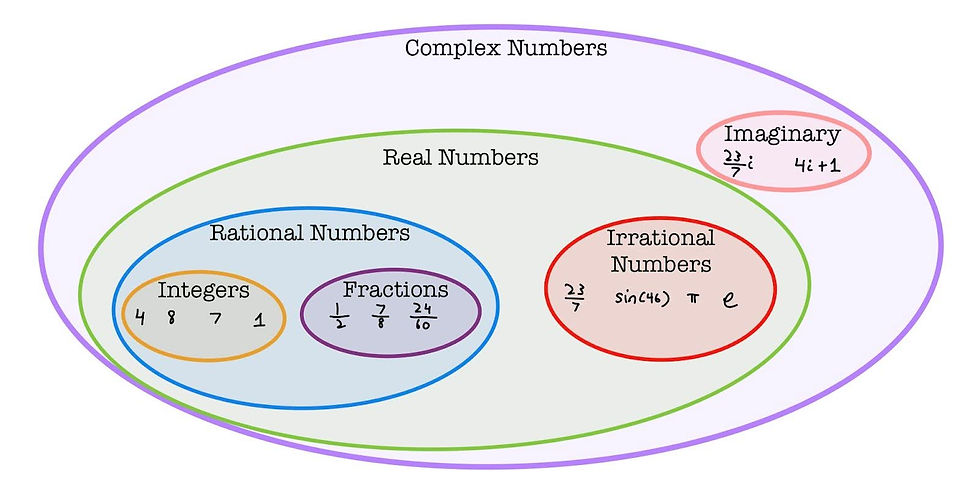
In ancient times, mathematicians only worked in integers and eventually rational numbers — these were numbers that could be easily visualised, as we could count integers and rational numbers were fractions of integers. The Greeks began to discover certain equations which had no rational solutions, and these numbers were at first perplexing. Eventually, these irrational numbers were studied in more detail, and became a familiar commodity. These numbers together formed the set of real numbers. 

As methods developed, mathematicians began to solve quadratic and cubic equations — equations with multiple solutions. This was before the development of modern algebraic notation (formally introduced by Viete and Descartes in the late 16th and early 17th centuries), when geometric approaches were most often used. Some of the developed equations were found to not have solutions that were solvable using geometric approaches — sometimes this was due to negative lengths (which were not familiar during that time) or complete breakdowns of shapes. The latter of these were regarded as impossible problems for thousands of years. 

This problem reoccurred in the 1500s, when Cardano began to study and solve the depressed cubic, a simplified form of the general cubic equation. Cardano developed and created his own formula by visual means: he used an image of a cube, and then based on the cube’s solution, transcribed a formula to solve for the depressed cubic. [1]

Cardano’s formula uses multiple roots in certain depressed cubics where some values such as c and d are negative. When the values are plugged into the formula, it produces solutions that involve negative roots. This portion remained true for many hundred years, slowly evolving in terms of their acceptance as they were being used more often. Later mathematicians like Bembelli and Euler came to define that √-1 is i so that mathematicians could easily work on their problems without having to worry about arithmetic logic. 

This perplexing number was defined to solve the equation i² = -1,  and the positive root of this equation √-1 was called i, the imaginary constant. All real multiples of i were called imaginary numbers, and when combined with a real number (eg: 3 + 4i), they were called complex numbers. 

Imaginary numbers can be represented on a complex plane where the x-axis is represented by real numbers and the y-axis is formed by imaginary numbers. As an example, 5 - 2i as below on the complex plane:

[6]

Representing Complex Numbers

Complex numbers can be represented by 2 parts: 

a + bi

where a and b are real numbers and a would be the real part and bi would be the imaginary part.

Understanding The Arithmetics

The fundamentals of understanding and applying these complex numbers would include appreciating the common arithmetics as they relate to imaginary numbers[2][5][4]:

Addition: (a + bi) + (c + di) = (a + c) + (b + d)i

Multiplication: (a + bi)(c + di) = (ac − bd) + (ad + bc)i

Division: Some simple divisions are outlined as below

ai/bi = a/b

ai/b = ai/b 

a/bi = a/bi

Here’s more of a complicated example:

To proceed, we need to multiply the fraction by the denominator conjugate, this might remind you of rationalising surds:

Keeping in mind that i² = -1, when we simplify down the fraction we get:

Taking one step further to apply these in real life scenarios, it’s important to understand this in through polar representation as shown below:

[7]

To find |z|, we need to think of solving it like using the Pythagorean theorem. Looking at the diagram above we can take the values of a and b from the complex number a + bi and substitute it into the pythagorean formula: c² = √(a² + b²), c² in our case being |z|. Once we substitute and simplify, we have solved our distance.

In the complex plane, we can represent complex numbers as points in space, with the real part corresponding to the x-axis value and the imaginary part corresponding to the y-axis value. This allows us to visualise and work with complex numbers as we would standard cartesian coordinates, and together with polar and exponential forms, means we can express them in multiple ways to suit certain problems and perspectives.

Use of Complex Numbers in Real World Applications

Visualising complex numbers as points in space in various ways helps us explore their geometric interpretations, such as rotations, transformations, and even fractals. This opens up new possibilities for mathematical exploration and applications in fields like physics, engineering, and computer graphics.

But before we dive into modern applications, we need to understand its infamous theoretical application: Schrodinger’s Wave Equation. 

[8]

In the world of quantum physics, Schrodinger’s Wave Equation remains to be one of the most important and influential equations in the world of physics. One of the most important parts of the equation itself is i, which shows its significance in the real world. One common application of Schrodinger’s Wave Equation is in electrical engineering, where they are used to represent the voltage and current in alternating current (AC) circuits as they need to use i when calculating and dealing with the electrical waves. AC voltage and current waveforms are very similar to sine curves in a graph, and they are described using complex numbers. By using complex numbers, engineers are able to analyse and design AC circuits with ease.

Imaginary numbers are also used extensively in signal processing to analyse and manipulate signals, such as sound and images. Complex numbers can be used to represent signals that have both a magnitude and a phase, and they can be transformed using techniques such as Fourier analysis. Common examples in the manipulation of sounds and images are in movies when directors use computer-generated imagery (CGI), and in video games when your character's 3rd person viewpoint moves and changes around.  They also help us process sound waves which also use the aforementioned Schrodinger’s Equation, allowing us to create amazing 3D audio experiences. [4]

Complex numbers also come in handy when creating 2D and 3D graphics. For instance, we can use them to represent points on the screen or handle rotations and movements of objects in the game world. Additionally, they help us make physics simulations more realistic. Things like fluid motion and waves can be beautifully expressed using complex numbers, bringing more life and realism to the game. In the audio world of games, complex numbers also play a crucial role.

One example in the gaming world is the blockbuster Grand Theft Auto V or GTA V released in 2013. Being the most expensive game to develop at that time, it had a number of flaws including water physics in the game — it would not move when a character swam in it. I am confident as developers work on GTA VI which is due to be released next year, the water will move more realistically as they will apply quaternions (which consists of four components expressed as a + bi + cj + dk where a,b,c and d are real numbers whilst i, j and k are imaginary components). These quaternions [3] are akin to coordinates in a 4-D space. This elegant set of numbers also has other applications in chemistry and physics, and forms a group under multiplication, a set of numbers with fascinating symmetry properties and classification abilities. 

In conclusion, imaginary numbers are a type of complex number that have many practical applications in various fields. They are a powerful mathematical tool that helps us understand and design complex systems. By using imaginary numbers, engineers and scientists can analyse and manipulate complex phenomena, making them an essential tool for innovation and discovery.

---

References:

1. How Imaginary Numbers Were Invented. (2021, October 31). YouTube - Veritasium. [1] https://www.youtube.com/watch?v=cUzklzVXJwo

2. C. Complex Numbers. (N/A). M.I.T. 18.03 Ordinary Differential Equations 18.03 Notes and Exercises - Arthur Mattuck [2]

3. Quaternions: What Are They, and Do We Really Need Them? (2022, August 20). The STEM Bulletin - Zhongyi Ho [3]

4. Imaginary Numbers, Functions of Complex Variables: 3D animations. (2015, October 27). YouTube. https://www.youtube.com/watch?v=bIY6ahHVgqA - Physics Videos by Eugene Khutoryansky [4]

5. Complex Numbers (Definition, Formulas, Examples). (n.d.). BYJUS. [5] https://byjus.com/maths/complex-numbers/

6. Complex Numbers and Polar Coordinates - dummies. (n.d.). Complex Numbers and Polar Coordinates - Dummies. [6] https://www.dummies.com/article/academics-the-arts/math/pre-calculus/complex-numbers-and-polar-coordinates-262652/

7. Frederick Roberts, D. R. (n.d.). Graphing Complex Numbers - MathBitsNotebook (A2). Graphing Complex Numbers - MathBitsNotebook (A2). [7] https://mathbitsnotebook.com/Algebra2/ComplexNumbers/CPGraphs.html

8. File:SchrodingerEquation.JPG - Wikipedia. (n.d.). File:SchrodingerEquation.JPG - Wikipedia. https://en.wikipedia.org/wiki/File:SchrodingerEquation.JPG. [8] https://en.wikipedia.org/wiki/File:SchrodingerEquation.JPG

9. A2 Level Math: Complex Numbers 2.1 - Introduction. (2018, May 17). YouTube - Huzaifa Usman. https://www.youtube.com/watch?v=fO8-g01wjx8

10. A2 Level Math: Complex Numbers 2.2 - Conjugates. (2018, May 17). YouTube - Huzaifa Usman. https://www.youtube.com/watch?v=eacAwvrBkmM

11. Imaginary Numbers (Definition, Rules, Operations, & Examples). (n.d.). BYJUS. https://byjus.com/maths/imaginary-numbers/

12. Kidwell, E. (2015, June 18). Imaginary Numbers. Maths Careers - Eugene KIdwell. https://www.mathscareers.org.uk/imaginary-numbers/