top of page
Search

The Physics Behind Flow, Flight and F1

  • Zhang Ning Chia
  • Apr 4
  • 4 min read

By Zhang Ning Chia


Among the vast array of principles and formulas that the world of physics and engineering offers, Bernoulli’s principle stands out as a cornerstone concept of fluid dynamics, linking the intricate relationship between pressure, velocity, and height in governing fluid behavior. Named after Swiss mathematician and physicist Daniel Bernoulli in 1728 (Wikipedia Contributors, 2019), it states that “an increase in the speed of a fluid occurs simultaneously with a decrease in pressure or a decrease in the fluid's potential energy”, a concept that can be mathematically expressed with Bernoulli’s equation. 



Deriving Bernoulli’s equation

At its core, Bernoulli’s Equation is a direct manifestation of the law of conservation of energy (as is everything). By applying this fundamental principle, we can derive Bernoulli’s Equation.

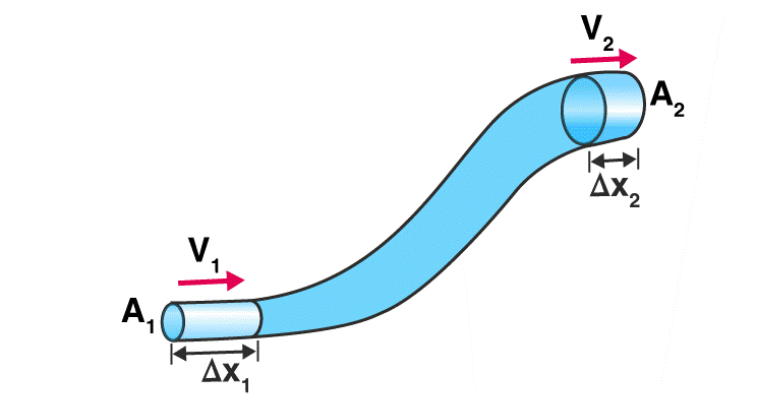
Fig 1: a malleable pipe with changing area and height
Fig 1: a malleable pipe with changing area and height

Let the pressure entering the pipe be P1 and the height above the ground be h1. Similarly, let the pressure exiting the pipe be P2 and the height above the ground be h2. 


To begin, energy in must equal energy out. The input energy at the beginning of the pipe would be the sum of the work you input, the potential energy at that point, and the kinetic energy at that point. This is equal to the output energy. 

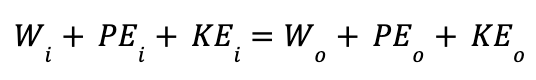
Since work is defined as force multiplied by distance, it can also be expressed as pressure multiplied by the volume of fluid displaced over time. By incorporating the relationship between density and mass (where density is mass per unit volume), we arrive at the following expression:

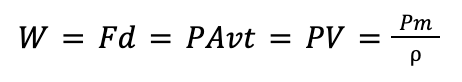
The equations of kinetic energy and potential energy do not need further manipulation for us to form Bernoulli’s equation. By simply rewriting our initial expression, we obtain:

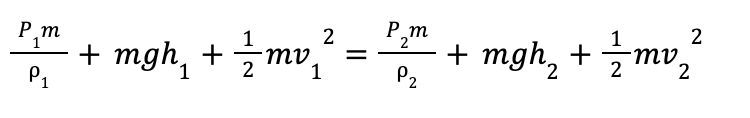
Since mass is conserved and remains constant throughout the system, it can be canceled out. Finally, by multiplying each term by density, we derive Bernoulli’s Equation, which is expressed as:

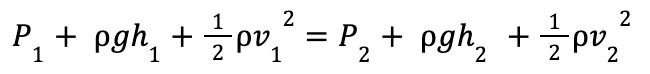
(LibreTexts, 2016)



How planes fly

One of the most well-known applications of Bernoulli’s Principle is in aerodynamics, particularly in how airplanes achieve lift. The airfoil of the plane (the wing) is designed to ensure that the air flows faster over the curved upper part of the wing than along the flatter bottom surface. The faster airflow over the top decreases pressure compared to the slower-moving air below (SKYbrary, 2021).

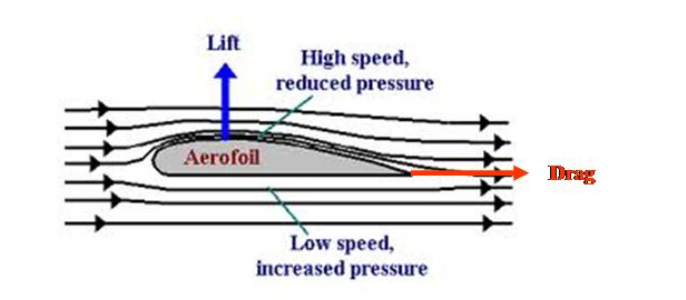
Fig 2: a plane’s airfoil, side view (SKYbrary, 2021)
Fig 2: a plane’s airfoil, side view (SKYbrary, 2021)

Thinking in terms of Bernoulli’s equation, we can rationalize this easily. The potential energy component remains the same both before and after as we are remaining at a constant height and thus cancels out. If the speed at the top, which we will call v1, is higher than v2, the speed at the bottom, P2 would have to increase to compensate and balance the equation. This pressure difference generates lift as there is a force under the airfoil that counteracts gravity thus allowing the aircraft to fly. 



How F1 cars don’t fly

Downforce is a critical concept in Formula 1. At first, it may seem counterintuitive as after all, heavy emphasis is placed on reducing a car’s weight in order to optimize performance. However, the importance of downforce quickly becomes apparent. By generating greater downforce, an F1 car is firmly pressed onto the track, significantly enhancing grip. This increased traction allows drivers to navigate corners at higher speeds without losing control. Without sufficient downforce, the immense speeds at which F1 cars travel would cause them to lose stability and spin off the track, making precise handling nearly impossible.


The concept of “wings” is also used to create downforce in F1 cars. The front and back wings of an F1 car are like airplane wings, just turned upside down for the force to push downwards instead of up (Why F1 cars have wings – with a McLaren Aero Specialist, 2024). Furthermore, the floor of an F1 car plays a pivotal role in generating what is known as the ‘ground effect’, which creates a powerful suction-like force. Unlike traditional wings that generate downforce at the cost of increased drag, the underfloor aerodynamics of an F1 car are designed to exploit the Venturi effect, a principle derived from Bernoulli’s Equation. This allows for immense downforce while maintaining aerodynamic efficiency.


The Venturi effect describes how a fluid’s velocity increases as it passes through a constricted space, causing a corresponding pressure drop. In an F1 car, the carefully sculpted underfloor tunnels, known as Venturi tunnels, force incoming air through a narrowing passage before gradually expanding again. As the air accelerates through these tight sections, its pressure decreases, creating a low-pressure zone beneath the car. Since the pressure below the car is now lower than the atmospheric pressure above, the car is effectively "sucked" down onto the track (Red Bull Racing, 2022).



Limitations:

While Bernoulli’s Equation is immensely useful, it has its limitations. It assumes that the fluid is incompressible and has no viscosity, which is not always realistic (Wikipedia Contributors, 2019). In real-world applications, factors such as turbulence, friction, and external forces can affect fluid behavior, requiring corrections or more advanced equations like the Navier-Stokes equations. The principle, however, is still deeply embedded in our daily lives and has many more applications that we have not discussed. Despite its limitations, by mastering Bernoulli’s Principle, scientists and engineers continue to innovate and optimize fluid systems that enhance efficiency and functionality in various industries.




References: 


Comments

bottom of page